|
SOLVIA Material Library
The following material models are available for stress analysis in SOLVIA:
ELASTIC and ORTHOTROPIC Material Models
The stress-strain relationships are defined by means of constant Young's moduli and Poisson's ratios. In orthotropic analysis, the axes of orthotropy can be generated and can be different for each element.
NONLINEAR-ELASTIC Material Model
The nonlinear elastic material behavior is defined by specifying the stress as a piece-wise linear function of the current strain.
THERMO-ELASTIC Material Model
The Young's modulus, Poisson's ratio and the mean coefficient of thermal expansion vary as a function of temperature.
TIME-ELASTIC Material Model
Primarily for use in load case analysis where each load case is linear but where load cases may have different material parameters, for example different E-modulus. Time functions may then be used to scale the parameters to their appropriate load case values and all load cases can be analyzed in one run without any restarts. The TIME-ELASTIC material model may also be used together with the element BIRTH/DEATH option to simulate, for example, a building process where elements are successively added and where the material parameters may be different in the various linear stages.
THERMO-ORTHOTROPIC Material Model
In addition to the capabilities of the ORTHOTROPIC model constant thermal expansion coefficients in the directions of the axes of orthotropy can be specified.
LAMINATE Material Model
The laminate material is used with the SHELL element and consists of any number of layers of different material properties. Shear stresses in the thickness direction are modified using 3-D theory to obtain continuity between layers and zero values on the top and bottom surfaces.
CURVE-DESCRIPTION Material Model
The instantaneous bulk and shear moduli are defined as a function of the volumetric strain. The material tensile failure is modeled using tension cut-off conditions.
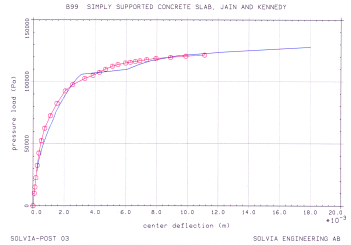
CONCRETE Material Model
The multi-axial stress-strain relation is defined by using for the principal stress directions a uniaxial stress-strain relation that is modified for biaxial and triaxial stress conditions. The material tensile failure, compression crushing, and post-failure behavior including strain-softening conditions are modeled.
|

|
DRUCKER-PRAGER Material Model
Flow theory of plasticity is used with the Drucker-Prager yield surface, a cap and a tension cut-off criterion.
PLASTIC and PLASTIC-MULTILINEAR Material Models
The plasticity relations are based on the Prandtl-Reuss equations. Multi-linear isotropic and kinematic hardening, small or large deformation conditions can be analyzed.
PLASTIC-CREEP Material Model
The material is described using the Prandtl-Reuss equations for plasticity. The yield stress, Young's modulus, hardening modulus, Poisson's ratio and coefficient of thermal expansion are temperature-dependent. Linear isotropic or kinematic hardening is assumed. Creep strain accumulation in cyclic loading conditions is taken into account using auxiliary hardening rules. The general model can be specialized to THERMO-PLASTIC or CREEP only analysis.
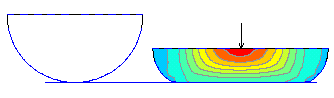
RUBBER Material Model
The stress-strain relationship of this hyper-elastic rubber model is defined using the Mooney-Rivlin constants.
| |
Oil Material Model
The viscosity is temperature and pressure dependent. The material is used with the FILM element in the finite element discretization of Reynolds equation. See Oil Film Applications (PDF).
Mixed Interpolation
The PLANE and SOLID element types can be used with mixed interpolation of element displacement and pressure for nearly incompressible analysis, for example of plasticity and rubber materials.
User-Supplied Material Model
The SOLVIA program provides also an option whereby the user can program for the PLANE and SOLID elements through an interface an own material model, which may include time and temperature effects. The interface is designed so that the user can program directly complex linear or nonlinear material models with relatively little knowledge of SOLVIA. The user-supplied material option is not available in executable-only program versions.
| 